Are you ready to challenge your brain with a fascinating math puzzle? At first glance, the equation in the image may look like a simple addition problem, but there’s a hidden pattern that makes it more complex than you think.
Take a moment to analyze the given equations:
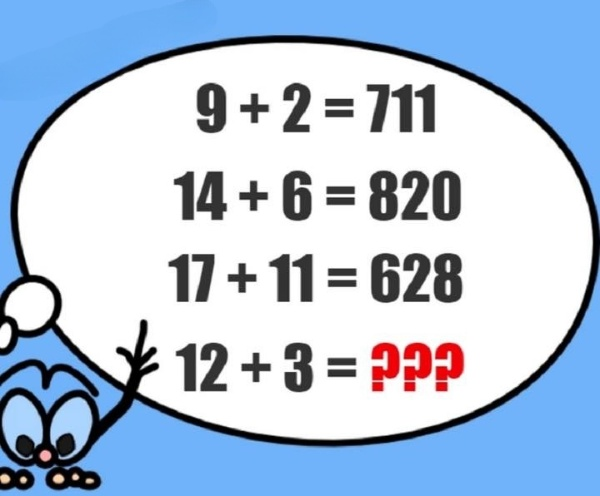
- 9 + 2 = 711
- 14 + 6 = 820
- 17 + 11 = 628
- 12 + 3 = ???
Can you figure out the logic behind these numbers and find the correct answer? Give it a try before scrolling down for the solution!
Common Mistakes People Make When Solving This Puzzle
Many people approach this problem using traditional math rules. Since the equations involve addition, they naturally assume the answer follows basic arithmetic. However, these numbers don’t add up conventionally, leading to confusion.
Here are some common errors people make:
✔ Trying to use standard addition – When adding 9 + 2, the result should be 11, but the puzzle gives 711 instead. Clearly, something else is happening.
✔ Assuming a hidden multiplication or division – Some people think there’s a multiplication or division pattern involved, but that doesn’t explain all the numbers.
Video : if 2+9=711 then find 12+3=??? tricky number Puzzle with answer
✔ Overcomplicating the logic – Sometimes, the best approach is to look for a simple pattern instead of forcing complex mathematical operations.
If you’re stuck, don’t worry! Let’s break it down step by step and uncover the hidden pattern behind these numbers.
Step-by-Step Guide to Solving the Puzzle
To understand the logic behind these equations, let’s analyze how the numbers are structured.
Step 1: Look for a Pattern in the Results
Instead of performing normal addition, let’s break down each result:
- 9 + 2 = 711
- 14 + 6 = 820
- 17 + 11 = 628
Notice that each result consists of three digits. What could these numbers represent?
Step 2: Identify the Hidden Logic
Let’s analyze the relationship between the input numbers and the output:
- The first digit of the result seems to come from the sum of the two numbers.
- The last two digits of the result seem to come from the product of the two numbers.
Let’s verify this theory:
- 9 + 2 = 11, 9 × 2 = 18 → But the result is 711?
- Instead of 18, it looks like the product’s last two digits are considered.
- If we write 11 first, but take only the last two digits of 9 × 2 = 18, we get 711.
- 14 + 6 = 20, 14 × 6 = 84 → The result is 820.
- First part: Sum = 20
- Second part: Product = 84
- The final number is 820 (placing 20 first, followed by 84).
- 17 + 11 = 28, 17 × 11 = 187 → The result is 628.
- First part: Sum = 28
- Second part: Product = 187, taking the last two digits 87
- The final result is 628.
Step 3: Apply the Logic to the Missing Equation
Now, let’s use this pattern to solve 12 + 3 = ???
- Sum:
- 12 + 3 = 15
- Product:
- 12 × 3 = 36
- Final Answer:
- By following the discovered pattern, we place the sum first, followed by the last two digits of the product:
- 12 + 3 = 915
Final Answer: 915
So, the correct answer to the puzzle is 915!
Conclusion: Challenge Your Brain with More Puzzles
Did you figure out the pattern on your own, or did you need a hint? Either way, this puzzle is a great example of how thinking outside the box can help solve seemingly tricky problems.
Video : Math Puzzles With Answers Only Genius Can Answer
👉 Drop a comment below and let us know how long it took you to solve it!
👉 Share this puzzle with your friends and challenge them—can they solve it faster than you did?
👉 Try more brain teasers to improve your problem-solving skills and have fun while exercising your brain!
Math puzzles like these are excellent for boosting logical thinking and pattern recognition. Keep challenging yourself, and you’ll soon become a master at spotting hidden logic!
Celebrated country music singer, dies at 79 after Parkinsons battle….

A beloved figure from the music world, known for his sharp wit and satirical edge, has passed away at the age of 79, leaving fans in shock. This larger-than-life personality first gained fame in the early 1970s with a boundary-pushing, unconventional style that forever altered the landscape of country music. His provocative lyrics and fearless performances quickly earned him a loyal following, and he continued to surprise audiences with his bold approach to both music and life. His journey, which included a remarkable collaboration with one of the most iconic musicians of all time, was as unpredictable as it was unforgettable.
The late singer first rose to prominence with his satirical country band in the early ’70s, delivering unforgettable hits like “They Ain’t Makin’ Jews Like Jesus Anymore” and “Get Your Biscuits in the Oven and Your Buns in the Bed.” Although the band’s time was brief, his solo career flourished, and he embarked on a two-year tour with Bob Dylan, solidifying his place in music history.
Kinky’s colorful career extended beyond music. In 2006, he made headlines by running for governor of Texas, challenging incumbent Rick Perry. Although he finished fourth, his candidacy drew widespread attention and showcased his unique approach to politics. He later ran for the Democratic nomination for agriculture commissioner in 2010 and 2014, continuing his unconventional forays into public service.
A close friend, Clive Hattersley, fondly remembered Kinky as “an extraordinary communicator who could stir deep emotions—whether through laughter or tears.” Hattersley also revealed that Kinky had been quietly battling Parkinson’s disease in the years leading up to his death.
Throughout his prolific career, Kinky released 18 albums, with his final one, Circus of Life, arriving in 2018. His legacy of wit, music, and unapologetic authenticity will endure, leaving a lasting imprint on both his fans and the world of satire.



Leave a Reply